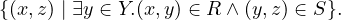
Definition 1 (category). A category C consists of:
such that:
Definition 2 (initial and terminal object). An object X in a category C is initial if, for every object Y , there is exactly one morphism from X to Y . This means that C(X,Y ) is the one-element set. An object Z is terminal if, for every object Y , there is exactly one morphism from Y to Z, i.e., C(Y,Z) is the one-element set.
Definition 3 (isomorphism). A morphism f ∈C(X,Y ) is an isomorphism if there is a morphism g ∈C(Y,X) such that g ∘ f = idX and f ∘ g = idY .
A directed multigraph (sometimes also called quiver) consists of:
Note that the edges are directed, i.e., E(a,b) is not necessarily the same as E(b,a), and many parallel edges are allowed.
Let G = (V,E) be a directed multigraph. The free category on G, (here) written FG, has V as objects and a morphism FG(X,Y ) is a sequence of consecutive edges, starting in X and ending in Y .
Show that FG is a category.
What are the isomorphisms in FG?
For which G does FG have an initial object? And when does FG have a terminal object?
The objects of the category REL are sets. For sets X and Y , an element of REL(X,Y ) is a relation between X and Y , i.e., a subset R ⊆ (X × Y ). The composition of relations R ⊆ (X × Y ) and S ⊆ (Y × Z) is given by
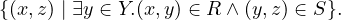 |
Can you define identities and prove that REL is a category?
What are the initial and terminal object of REL?
What are the isomorphisms?
The objects of SPAN are sets. A morphism between sets X and Y consists of a set Z together with a function f : Z → X and a function g : Z → Y .
The composition operation works in a similar way as for REL, but we don’t need an existential quantifier this time. Can you make this operation precise?
Can you prove associativity? Can you define identities and prove that SPAN is a category? What works or fails? (Hint: It only almost works. SPAN is a structure that is slightly weaker than a category, namely a bicategory.)
What are the initial and terminal object of SPAN?
What are the isomorphisms?
How does SPAN compare to the category REL?